EXAMPLES OF WORKING WITH DATA
Each of the examples is accompanied by a description and a link to the workbook with the implementation.
Using visual representation of data
Approximation of a complex curve by a polynomial Download
Polynomial dependencies are well suited for approximating complex curves with several inflection points. The Stamm program has a built-in function for finding the coefficients of a polynomial. Below is an example of approximation of an unknown function y=sin(x) by a polynomial. Let's write down 10 pairs of values x and y= sin(x) in columns A and B. Then we insert the function of finding the coefficients of the polynomial in cell D1 (Fig. 9.1).
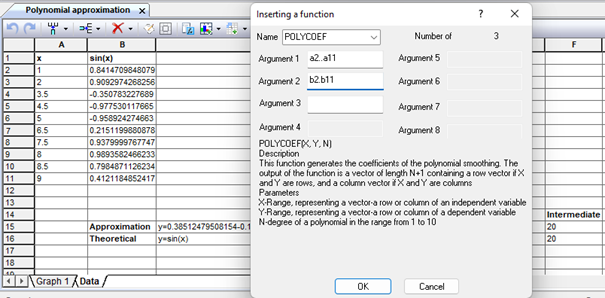
Figure 9.1. Inserting the function "POLYCOEFF" to find the coefficients of the polynomial
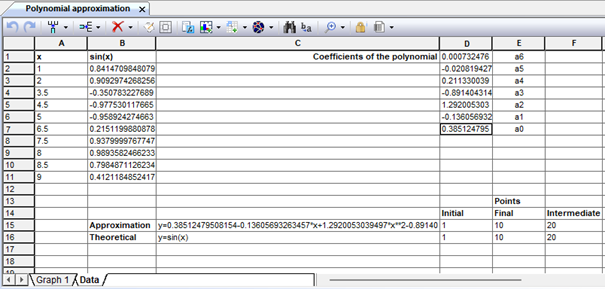
Fig. 9.2. Coefficients and equation of the smoothing curve
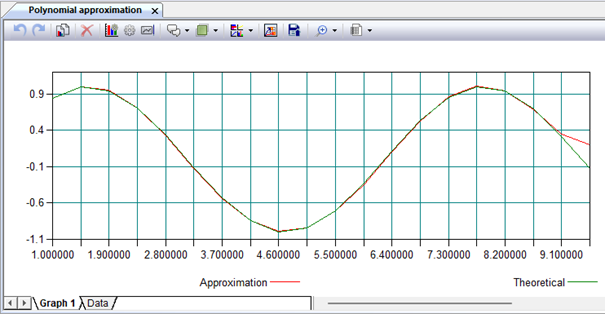
Figure 9.3. Smoothing the sin(x) function by a 6-order polynomial
Analysis of the failure rate of the ignition system Download
For any randomly selected product, it is impossible to determine in advance whether it will be reliable. Failure is an accidental event. Therefore, methods of probability theory and mathematical statistics are used to calculate reliability indicators. One of the conditional concepts used in the calculation of reliability indicators is "operating time". The operating time is the duration or amount of work of the product. For engines, the operating time is usually measured in kilometers of car mileage or in hours (motochas). In the technical and educational literature, you can find such expressions: daily operating time, operating time before the first failure, operating time between failures, etc. Below is an analysis of the failures of the ignition system with a Hall sensor. Experimental data on the operating time of this node are grouped into two blocks: failures in kilometers of the new node and node failures after the first repair, after which numerical data are entered in the workbook data sheet (Fig. 9.4). Moreover, the grouped data does not have to be oriented by rows or columns, so when constructing the frequency distribution, they will automatically be sorted in ascending order.
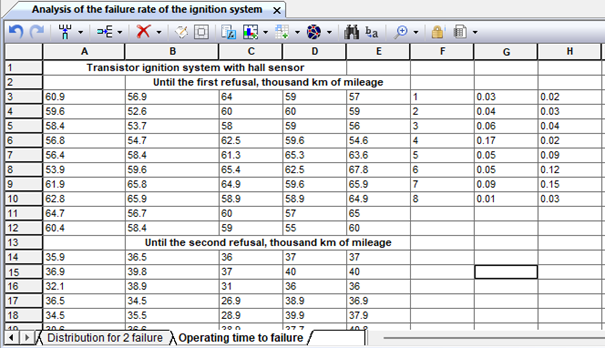
Figure 9.4. Data on failures of the ignition system with a Hall sensor in thousand km of mileage
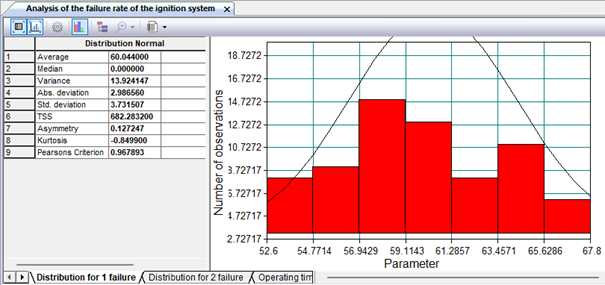
Figure 9.5. Histogram of failure rates of the new ignition system with Hall sensor (in thousand km of mileage)

Figure 9.6. Histogram of failure rates of the ignition system with Hall sensor after the first repair (in thousand km of mileage)
Predator-prey model Download
This example shows how to solve a differential equation representing a predator-prey model using a tabular model. We use functions for numerical solution of ordinary differential equations using Runge-Kutta integration methods with variable pitch. Consider a pair of first-order ordinary differential equations, known as the Lotka-Volterra equations, or the predator–prey model: dx/dt = x – αxy, dy/dt =−y + βxy. Let's denote x(t) the number of individuals of the prey population, and y(t) — the number of individuals of the predator population at time t. Let also v(t) be the growth rate of the prey population, and w(t) is the growth rate of the predator population. Consider the mathematical model "predator-prey", in which a limited growth model is used for a population of victims. v(t) = (a – bx(t))x(t) – сx(t)y(t); where (a – bx(t))x(t) sets the increase in the number of victims, – cx(t)y(t) – its reduction from being eaten by predators. w(t) = – dy(t) + fx(t)y(t). where – dy(t) sets the reduction in the number of predators due to mortality, fx(t)y(t) – its growth due to feeding by victims. Model parameters: a – coefficient of natural growth of the victim population (a > 0); b – mortality rate of victims from intraspecific competition (b > 0); c – mortality rate of victims from predators (c > 0); d – mortality rate of predators (d > 0); f is the coefficient determining the increase in the number of predators (f > 0). Let's put a blank sheet of a tabular simulation model in the book and create the appropriate cells to simulate population changes.
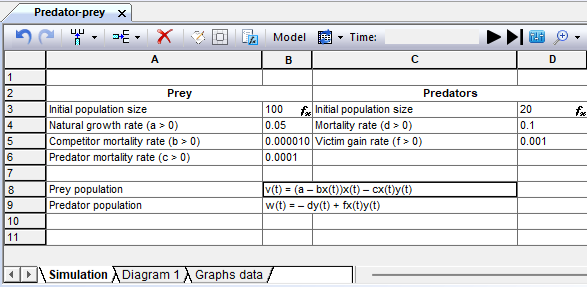
Figure 9.7. Sheet for imitation of the Predator-prey model
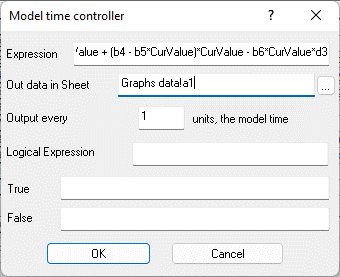
Figure 9.8. Properties of the controller cell to simulate a population of B3 prey
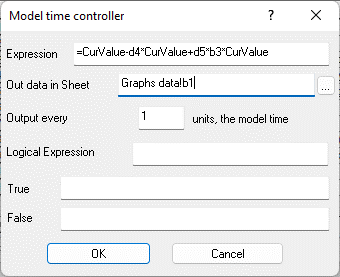
Figure 9.9. Properties of a controller cell to simulate a predator population D3
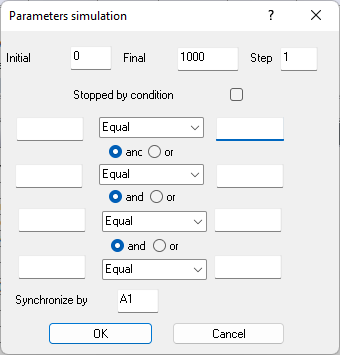
Figure 9.10. Model Parameters
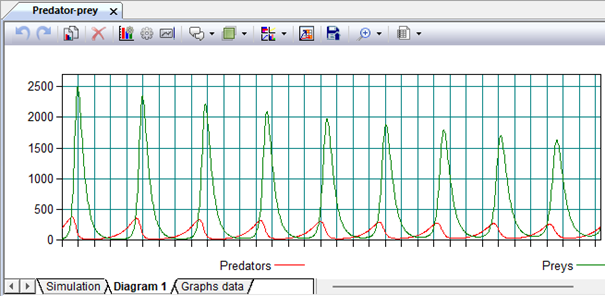
Figure 9.11. Graphical interpretation of the results
Statistical analysis
Forecasting of transportation from the warehouse of an industrial enterprise Download
For the period from 2017 to 2021, the volume of transportation of finished products from the warehouse of an industrial enterprise is known (Table 9.1). It is necessary to make a forecast of the volume of traffic in 2022. Table 9.1 Traffic volumes by year Period (year) 2017 2018 2019 2020 2021 Sales volume (thousand tons) 320 470 540 710 1025 Let's create a sheet with initial data in the workbook (Fig. 9.7).
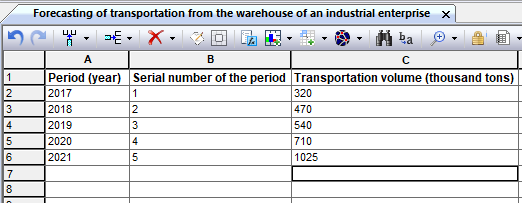
Fig. 1. A sheet with initial data on traffic volumes
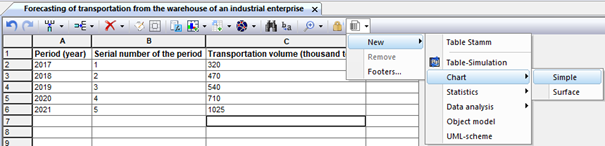
Fig. 2. The menu for selecting the type of graph
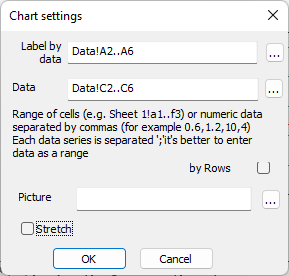
Fig. 3. Chart data range
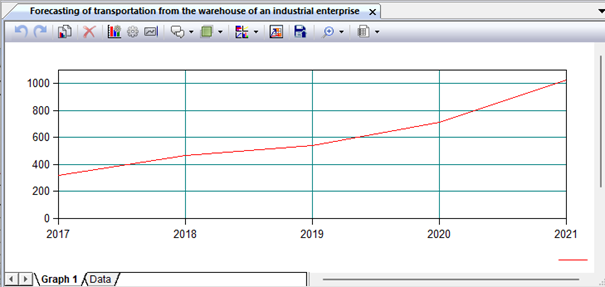
Fig. 4. Sketch schedule of traffic volume changes
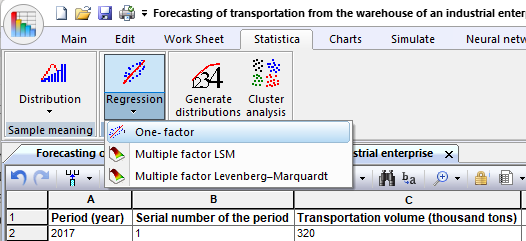
Fig. 5. Menu of the "Statistics" panel of the application feed
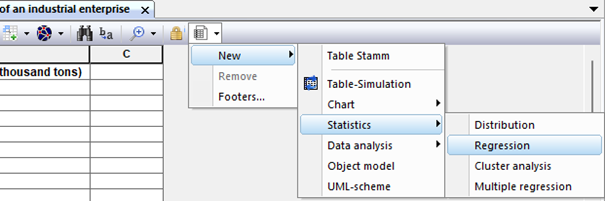
Fig. 6. Menu of the dashboard of the worksheet
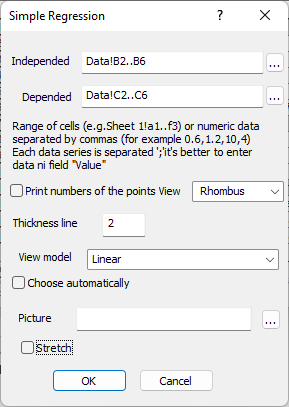
Fig. 7. Regression dependence settings panel
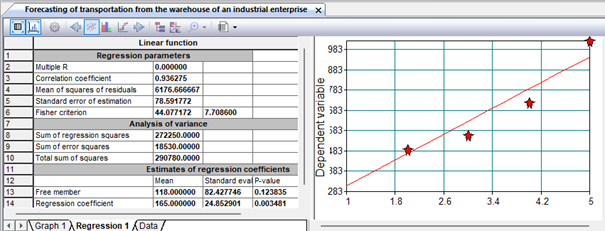
Fig. 8. Regression dependence parameters
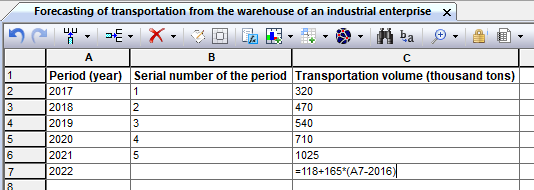
Fig. 9. Calculation of the regression dependence in the cell
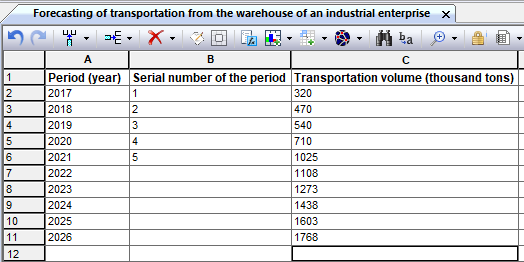
Fig. 10. Calculation of the traffic forecast for the prospective period
Obtaining parameters of multivariate regression dependence of the annual turnover of small enterprises on their characteristics by regions of Russia Download
The Internet provides statistical data on the indicators of small enterprises in the regions of Russia. Let's assume a linear view of the dependence of the turnover of small enterprises on their number in the region and the average number of employees. Let's perform a multivariate regression analysis using a linear mathematical model on the main effects in the Stamm system. Let's transfer the data to the Stamm worksheet (Fig. 9.100).
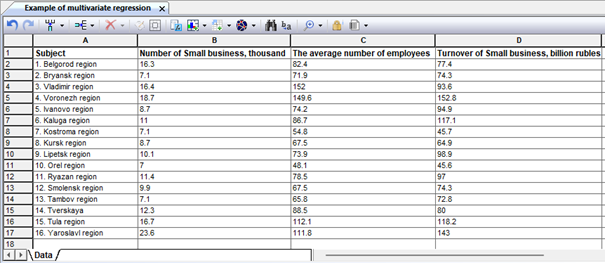
Figure 1. Initial experimental data
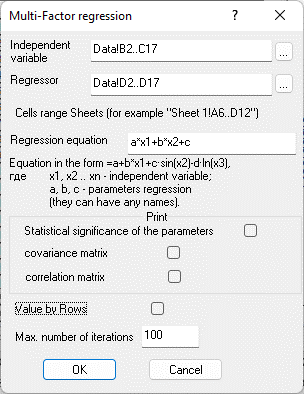
Figure 2. Regression analysis parameters panel
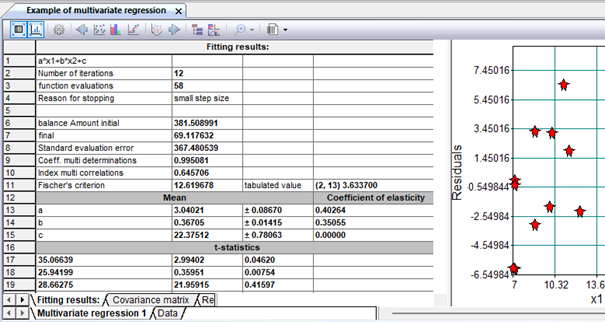
Figure 3. Approximation results
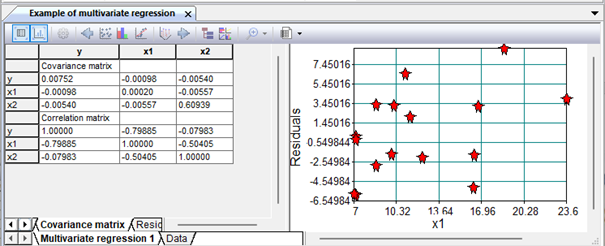
Figure 4. Approximation results
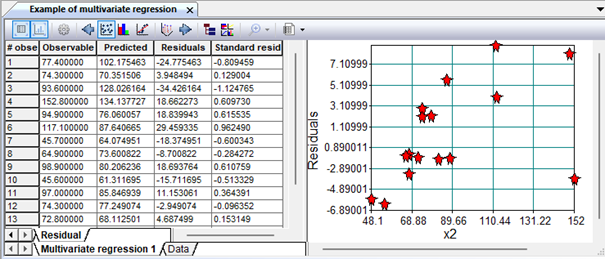
Figure 5. Covariance and correlation matrices
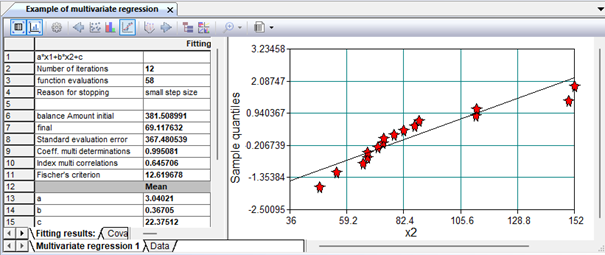
Figure 6. Residuals of the model
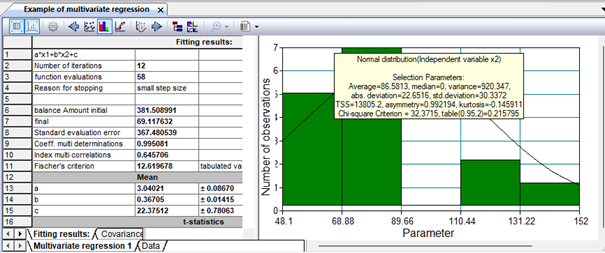
Figure 7. Estimation of the normality of the distribution using probability paper

Figure 8. Estimation of the normality of the distribution using the distribution function
Using simulation models of tabular type
Modeling of expenses related to car sales in the salon Download
The following example from the practice of a car dealership is posted on the Internet. In the last hundred months, the sales volume at the dealership ranges from 5 to 11 new cars per month. The salon manager orders 25 cars each time and makes a new order when the stock in the store is reduced to 10 cars. A new order can be made only after the previous one has been completed. We will simulate this strategy for 24 months. Let's perform a Monte Carlo simulation by setting car sales for a month by a random number with the given parameters of the distribution law.We believe that:
a) the initial stock is 30 cars
b) the cost of storing one car is 550,000 rubles per month.
c) one missed sale brings an average loss of 3,330,000 rubles.
d) one order costs 500,000 rubles.
Modeling tasks:
1. How many orders will have to be made in two years?
2. What are the costs associated with this strategy (thousand rubles)?
Let's create a new workbook and insert a simulation sheet there. Let's call it "Imitation of sales". In this sheet, we will create 6 special controller cells necessary for sales modeling (Fig. 9.12).
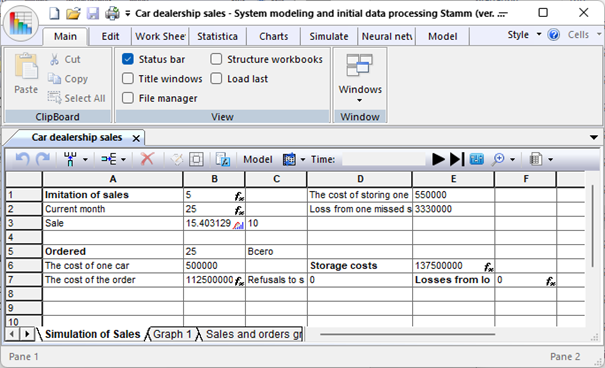
Figure 9.12. Simulation sheet for sales modelling
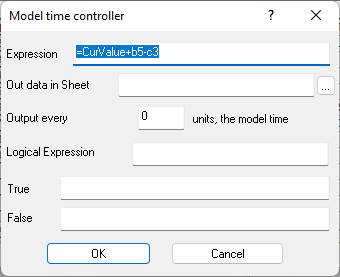
Figure 2. Formula in cell B1
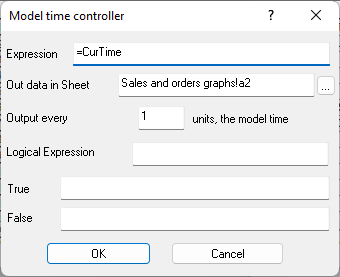
Figure 9.14. Formula in cell B2
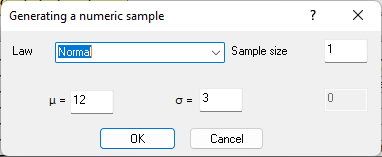
Figure 9.15. Formula in cell B3
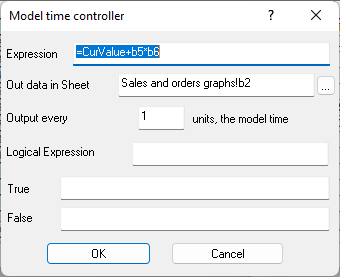
Figure 9.16. Formula in cell B7
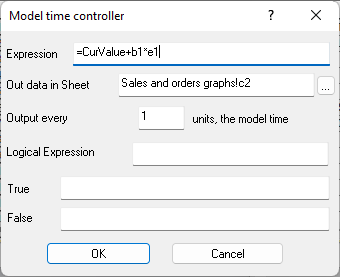
Figure 9.17. Formula in cell E6
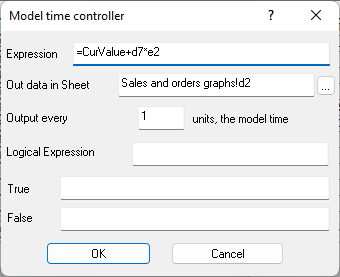
Figure 9.18. Formula in cell F7
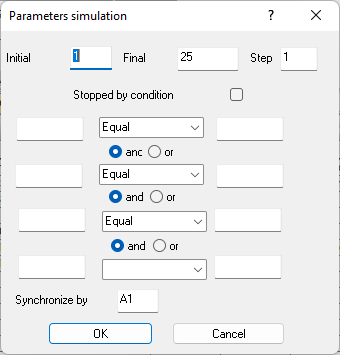
Figure 9.19. Model Parameters
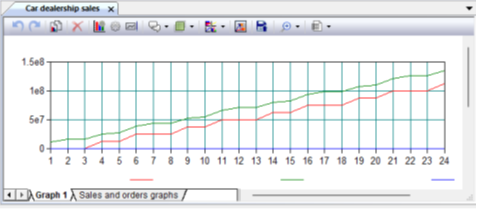
Figure 9.20. Cost change graphs

Figure 9.21. Simulation results
Modeling of repair of mechanisms in the workshop Download
The repair shop performs preventive inspection and repair of some mechanisms. Of all the mechanisms received by the repair service, 30% are mechanisms of type A, 50% – type B, 20% – type C. The mechanism of type A includes 10 parts that require inspection; the mechanism of type B includes six such parts, type C – four parts. The number of parts requiring replacement in each of the mechanisms can be any. For example, in a type A mechanism, the number of parts requiring replacement can range from 0 to 10 (with the same probability). For each replaced part, the customer pays the repair shop 5 den. units. In addition, the customer pays 10 monetary units for the inspection of mechanism A. units, for the inspection of the mechanism B – 8 monetary units, for the inspection of the mechanism C – 14 monetary units. Create an algorithm and a program (based on the Monte Carlo method) to determine the following values: – the probability that all parts will need to be replaced in the mechanism; – the average revenue of the workshop from the inspection and repair of one mechanism. The problem was solved using a macro written in VBA for Excel, implementing the Monte Carlo method. The implementation of this task in the Stamm system is presented below. The simulation sheet of the corresponding workbook contains 4 controller cells, which are random number generators distributed according to a given law, and 9 controller cells "Calculated expression" (Fig. 9.22).
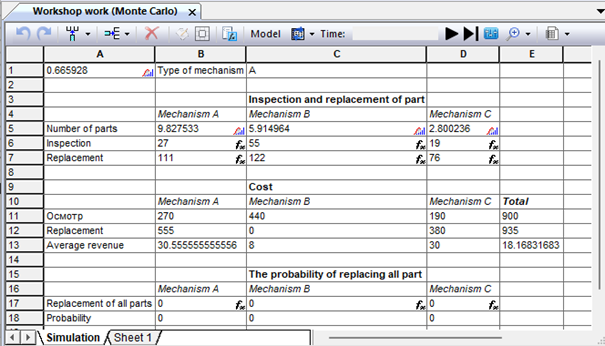
Figure 9.22. The sheet of simulation of inspections and replacement of parts
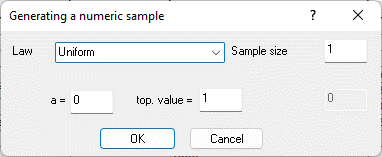
Figure 9.23. Controller cell B1
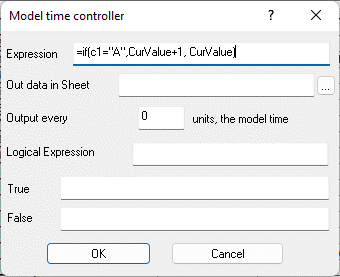
Figure 9.24. Formula in cell B6
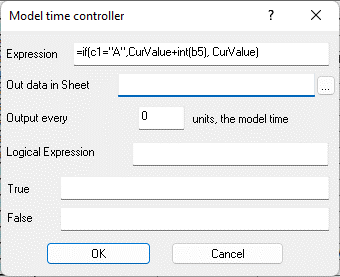
Figure 9.25. Formula expression in cell B7
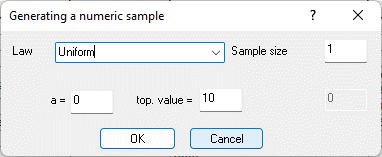
Figure 9.26. Generation of a random variable in cell B5
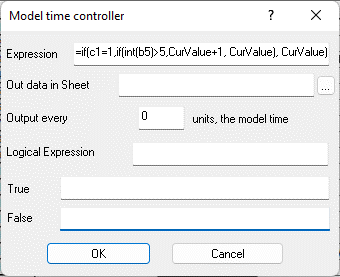
Figure 9.27. Formula in cell B17
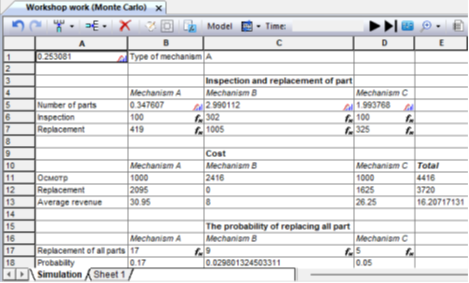
Fig. 9.28. Simulation results
Determination of the optimal fleet of vehicles for the delivery of goods from the wholesale base Download
Several variants of such a task are presented on the Internet, in general, its formulation is as follows. From the wholesale base, the products go on retail sale. Consumers are located in the city, where the wholesale base is located. The products received at the wholesale base should be processed and, if possible, delivered to consumers on the same day. If it is not fully exported, it remains at the base, thus creating losses associated with its storage. For simplicity, it is assumed that the auto enterprise and the base work seven days a week. The distance from the wholesale base to consumers is not set, but it is known that each of the machines can take out a given amount of cargo. The flow of products entering the wholesale base obeys the normal law of distribution. It is required to determine the optimal size of the fleet of machines needed to deliver products from the wholesale base to consumers. The criterion of optimality is the minimization of total costs, consisting of the costs of operating vehicles and the costs of cargo storage. The consumer service system is a discrete type system with a jump-like transition from one state to another at any event. For example, by changing the number of cars, you can change the cost of transporting goods, the speed of their delivery. The flow of incoming goods is irregular, therefore, the optimal ratio between cost groups can be established by selecting the law of management of service facilities (machines), and all the necessary values can be found analytically, without experiment. This analysis can be performed using the Monte Carlo method, which is the application of the procedure of "unlimited random sampling" of individual elements on a set in such a way that the probability of sampling each element is the same. The method is a simulation of an experiment to determine the probabilistic properties of a set of events. We will find such an optimal number of machines servicing the base, at which the total costs of transportation and storage will be minimal. The simulation sheet of the corresponding workbook contains one controller cell, which is a generator of random numbers distributed according to a given law, and 6 controller cells "Calculated expression" (Fig. 9.29).
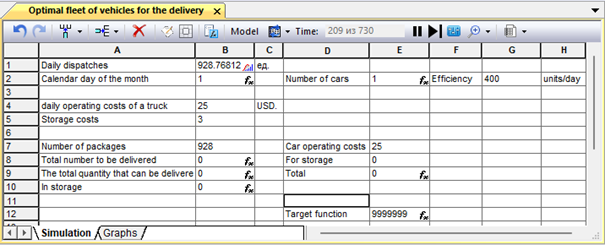
Figure 9.29. Modeling sheet of the optimal number of vehicles for the export of products
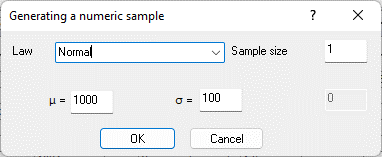
Figure 9.30. Controller cell B1
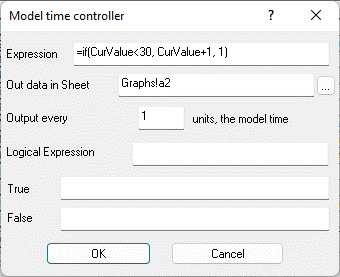
Figure 9.31. Formula in cell B2
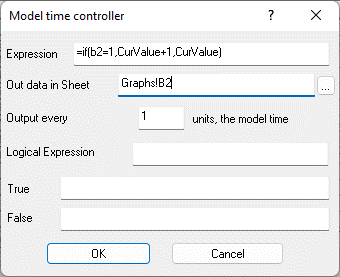
Figure 9.32. Formula in cell E2
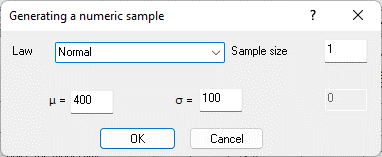
Figure 9.33. Formula in cell G2
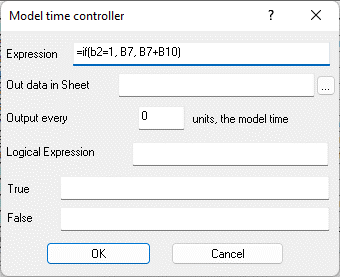
Figure 9.34. Formula in cell B8
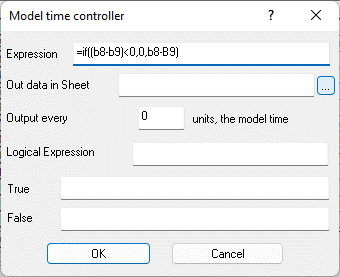
Figure 9.35. Formula in cell B10
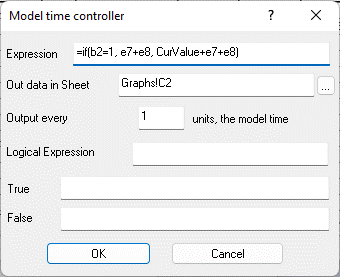
Figure 9.36. Formula expression in cell E9
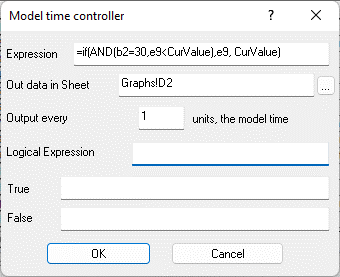
Рис. 9.37. Формула в ячейке E12
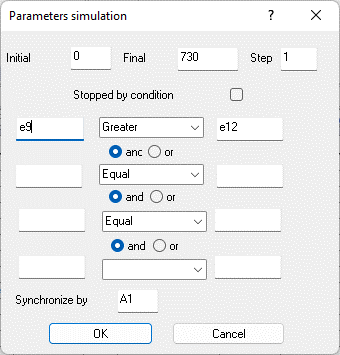
Figure 9.38. Model parameters
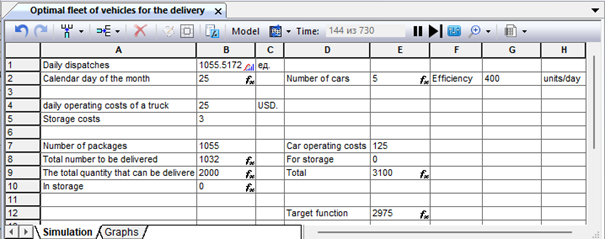
Figure 9.39. Simulation results
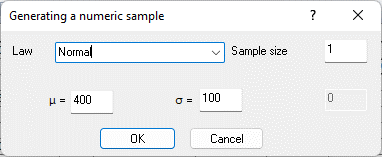
Fig. 9.40. Generation of a random output value in cell G2
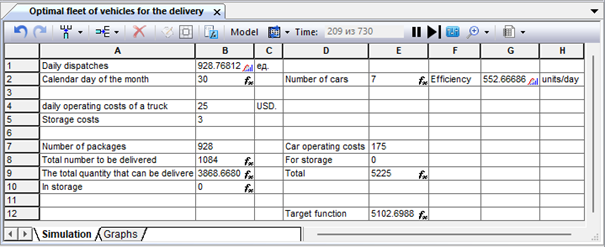
Fig. 9.41. The results of the model operation with the random nature of the car production
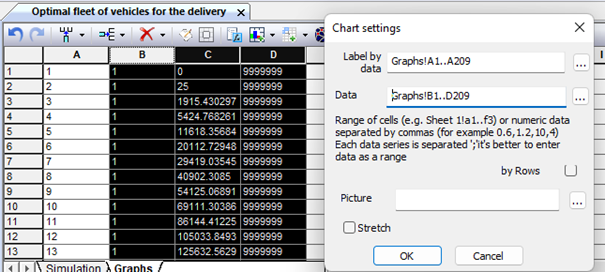
Fig. 9.42. Selecting data for plotting cost changes
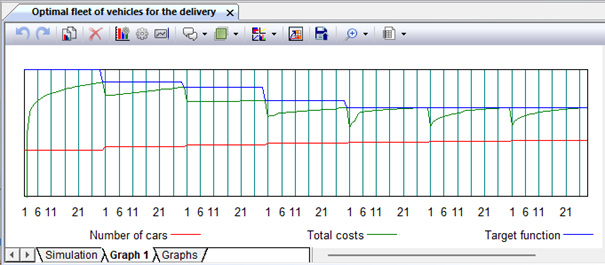
Fig. 9.43. Schedule of changes in delivery costs
Simulation of fuel consumption using a driving cycle profile Download
For some brands and models of cars, the dependences of the engine fuel efficiency indicators on the crankshaft rotation speed, load and other engine characteristics have been investigated and numerical values of the parameters of these dependences have been experimentally established. These dependencies are written in the language of the formula processor "Stamm", similar to ordinary equations, with the exception of variable references to other cells. When removing the speed and load profile of a typical driving cycle for a given make and model of car, it becomes possible to create models to simulate fuel consumption under the influence of various external conditions, for example, ambient air temperature, duration of stops with the engine running, etc. The speed and load profile of the driving cycles are set in tabular form in the form of a vector of values, the first coordinate of which is the time from the start of the cycle, and the second and subsequent parameters of the car are speed, crankshaft speed, throttle opening degree, etc. The speed profile of the driving cycle is set in a regular workbook sheet (Fig. 9.53).
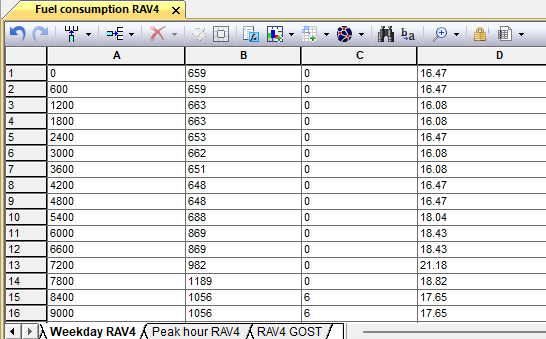
Fig. 9.53. Speed profile "Urban driving cycle"
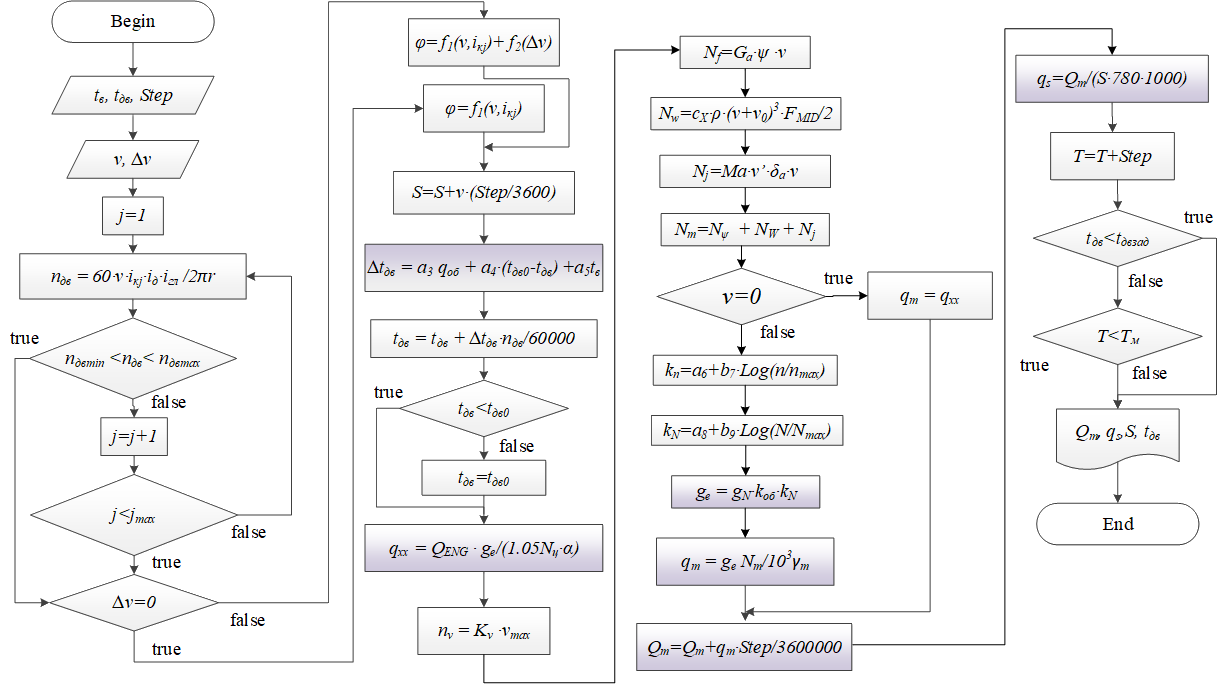
Fig. 9.54. Algorithm of the simulation model based on the profile of the driving cycle
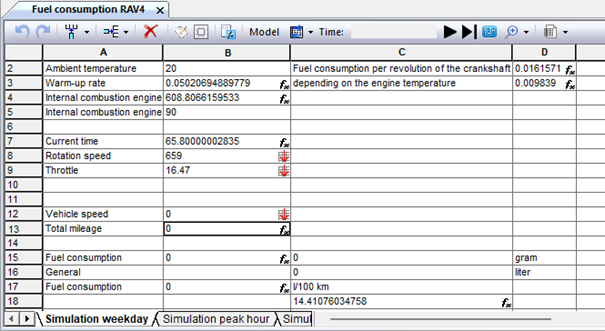
Fig. 9.55. Workbook "Modeling of fuel consumption"
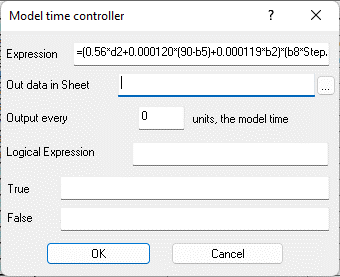
Fig. 9.56. Properties of the controller cell "Calculated expression" B3
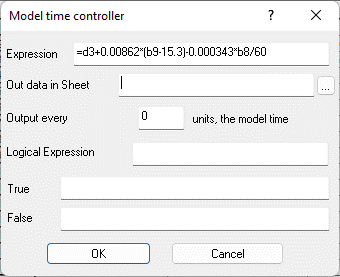
Fig. 9.57. Properties of the controller cell "Calculated expression" D2
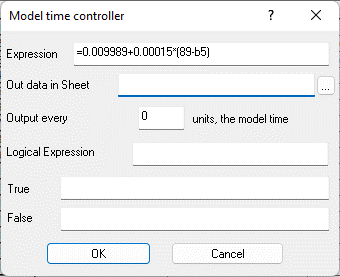
Fig. 9.58. Properties of the controller cell "Calculated expression" D3
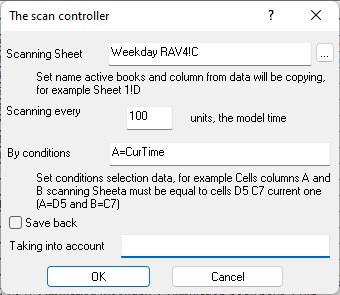
Fig. 9.59. Properties of the "Scan Controller" cell B12
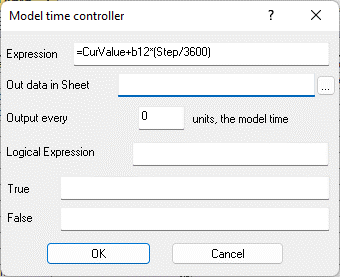
Fig. 9.60. Properties of the controller cell "Calculated expression" B13
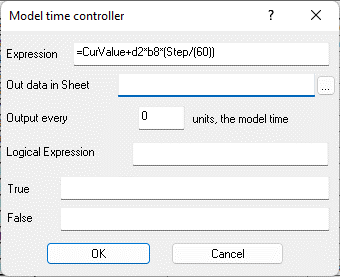
Fig. 9.61. Properties of the controller cell "Calculated expression" B14
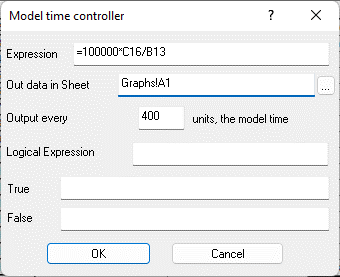
Fig. 9.62. Properties of the "Calculated expression" cell C17
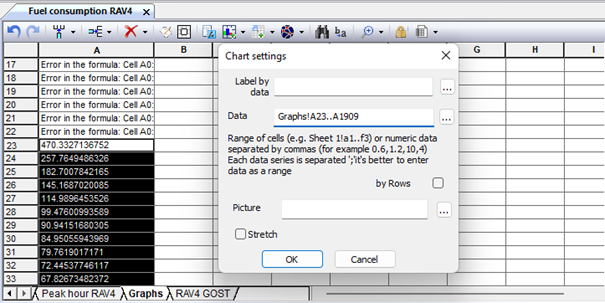
Fig. 9.63. Setting the chart parameters. Selecting a data range
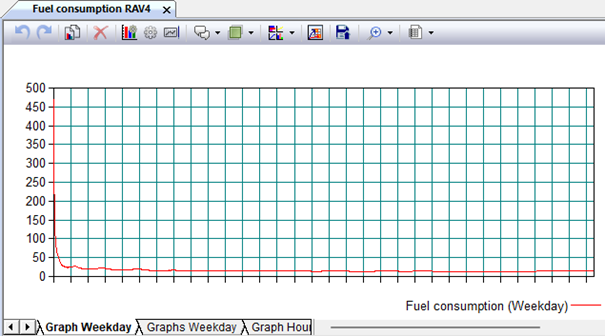
Fig. 9.64. Schedule of fuel consumption changes during simulation (Weekdays)
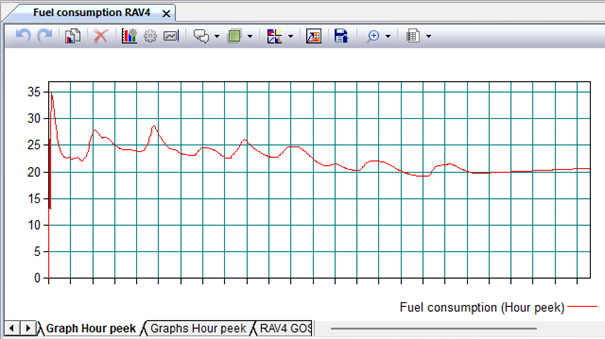
Fig. 9.65. Schedule of fuel consumption changes during simulation (Hour peek)
Simulation of the thermal state of the engine when warming up at idle Download
A simulation model of the process of warming up an automobile engine can be useful in determining the duration of warming up to a certain temperature of the coolant at a given ambient temperature and a different initial value. To obtain the amount of fuel consumption consumed for heating at idle under various external conditions. At the same time, the model does not use time profiles, although the value of the model time itself and its increment step are used for numerical integration when calculating the warm-up time, fuel consumption and some engine parameters. The sheet of the simulation model of the internal combustion engine heating is shown in Fig. 9.66. In the process of simulating idling, the engine operation mode is reproduced, set by the injection control controller of a real engine. This is achieved using experimentally obtained regression dependencies: the speed of rotation of the crankshaft and the degree of throttle opening on the temperature of the coolant and the external environment. These dependencies are implemented in cells B8 and B9 (Fig. 9.67, 9.68).
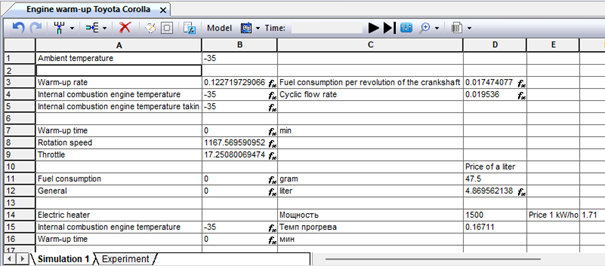
Fig. 9.66. Workbook "Warming up the Toyota Corolla internal combustion engine"
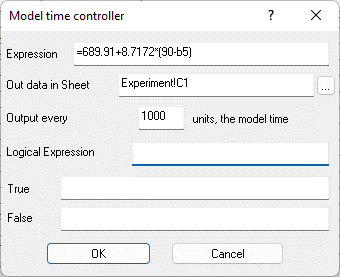
Fig. 9.67. Properties of the cell "Calculated expression" B8
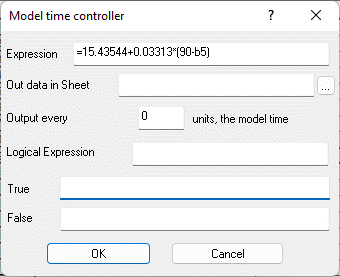
Fig. 9.68. Properties of cell B9
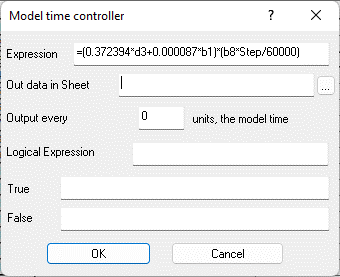
Fig. 9.69. Cell B3 "Calculated expression" - the rate of heating of the internal combustion engine coolant
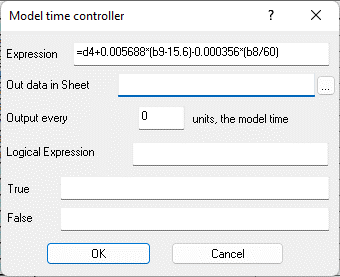
Fig. 9.70. Cell D3 "Calculated expression" - fuel consumption per revolution of the engine crankshaft
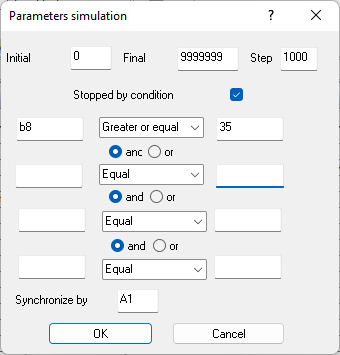
Fig. 9.71. Model parameters panel
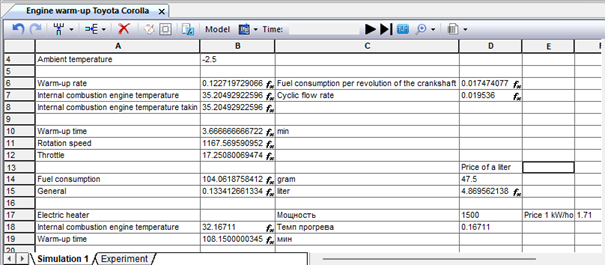
Fig. 9.72. Results of warm-up simulation
Improvement of transport logistics in the supply of spare parts of the helicopter fleet Download
UTair's helicopter fleet operates all over the world. Special units have been created to service helicopter equipment. One of them is the aircraft repair complex of UTair Engineering JSC, which carries out major repairs, maintenance, repair and restoration work on a wide range of helicopters of various classes. In addition, the company is the leading aviation and technical base of Mi-8, Mi8MTV-1, Mi-8AMT, Mi-10, Mi-26, Mi-171 helicopters and their modifications and performs services for the delivery to and from the repair of helicopters, aggregates by any means of transport. A significant part of the helicopter fleet is operated in the regions of the North of Siberia, which, in conditions of an insufficiently developed road network, significantly increases the costs of transport logistics of spare parts and aggregates. Analysis of the distribution of the raid during the year for MI-8 helicopters (Table. 9.3) shows that the average operating time per month during the year significantly depends on the time of year, and it is determined not only by weather and climatic conditions, but also by regional operating conditions.|
Calendar month
|
The raid in hours at the helicopter bases |
|||
|
Surgut |
Noyabrsk |
Tazovsky |
Novy Urengoy |
|
|
January |
50 |
40 |
45 |
20 |
|
February |
50 |
40 |
52 |
34 |
|
March |
50 |
45 |
54 |
40 |
|
April |
85 |
40 |
57 |
105 |
|
May |
90 |
35 |
76 |
100 |
|
June's |
90 |
30 |
73 |
110 |
|
July |
90 |
25 |
58 |
128 |
|
August |
90 |
25 |
63 |
100 |
|
September |
90 |
30 |
58 |
98 |
|
October |
90 |
40 |
60 |
98 |
|
November |
55 |
40 |
58 |
60 |
|
December |
40 |
35 |
55 |
70 |
The use of simulation modeling of the resource consumption of aggregates will allow predicting their delivery with higher accuracy and reduce logistics costs. We will build a simulation model of the delivery of the following spare parts of the MI-8 helicopter: - TV2-117 – aviation turboshaft engine, - main gearbox BP-8A, - main rotor hub HB. Losses due to the lack of replacement units, associated downtime of aircraft and storage costs in the warehouse are selected as the target function. A general algorithm for simulating the operating time of aggregates during the operation of aircraft, as well as the management of their supplies and the costs associated with this, is shown in Fig. 9.73.
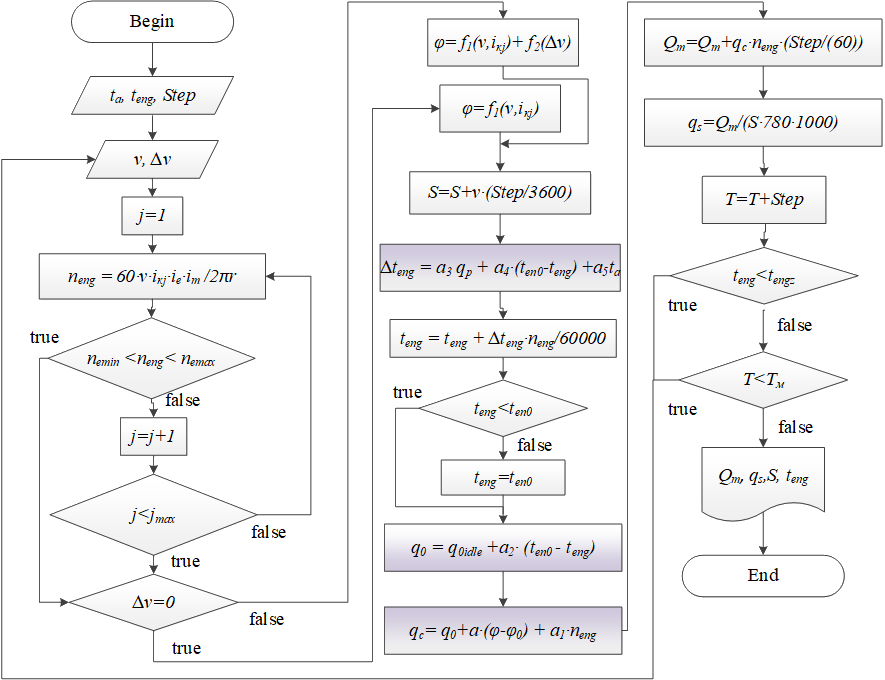
Fig. 9.73. Simulation model algorithm
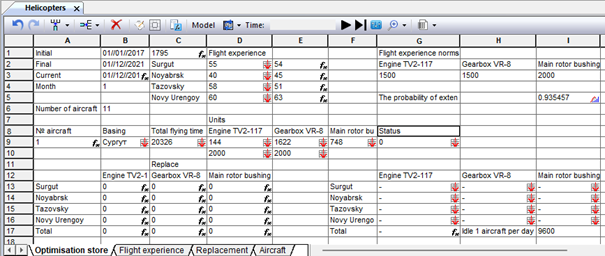
Figure 9.74. Simulation model sheet
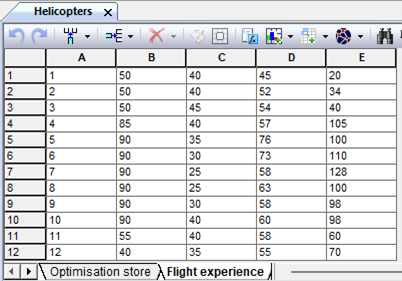
Figure 9.75. Helicopter flight simulation sheet
|
Type of controller cell |
Cell or range of the sheet |
Functions performed |
|
Model time scanning |
B3, C3 |
Determining the current calendar date based on the virtual time of the model |
|
E2:E5 |
Generation of a random value of the operating time of the aircraft during the month |
|
|
A9 |
Generating the current helicopter number |
|
|
B13:D16 |
Modeling of replacements by units and locations |
|
|
B17:D17 |
Calculation of the total number of replacements by aggregates for the entire simulation period |
|
|
G17 |
Data reset at the beginning of the month |
|
|
Scanning |
D2:D5 |
Simulation of the monthly flight of an aircraft depending on the location of the base |
|
B9 |
Displaying the location of the base |
|
|
C9 |
Simulation of the total flight of an aircraft |
|
|
D9:F9 |
Flight on individual aircraft units |
|
|
G9 |
The current status of the aircraft is "ready for operation", "needs replacement of the unit", "idle" |
|
|
|
G13:I16 |
Modeling planned replacements by month |
|
Random Number Generator |
I5 |
Generating the probability of extending the life of the unit |
The components of the model that provide the calculation of variables, the value of which changes over the course of the model time and depends on other variables of the model, are implemented as a simple controller of the model time (Fig. 9.76).
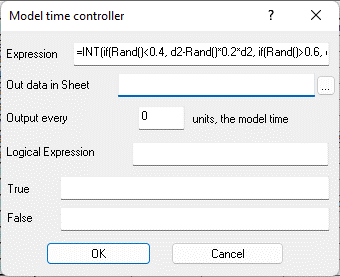
Fig. 9.76. The controller cell that calculates the average flight per month for this aircraft

Fig. 9.77. The controller cell determining the moment of replacement of the unit
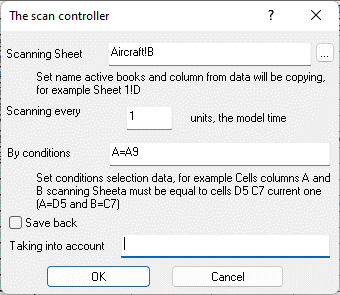
Fig. 9.78. A controller cell that scans the aircraft data table by the "Basing" column
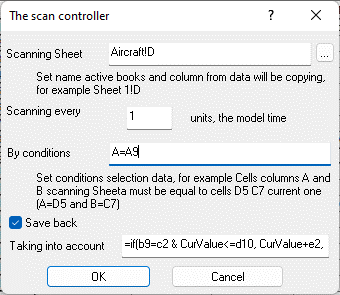
Fig. 9.79. The controller cell scanning the aircraft data table according to the column "Operating time TV-2-117"
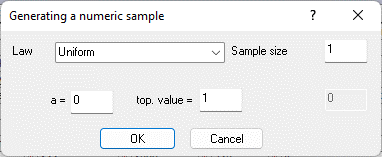
Fig. 9.80. A controller cell simulating the probability of resource renewal
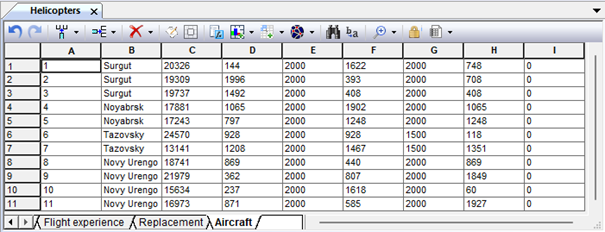
Fig. 9.81. Initial sample of the model
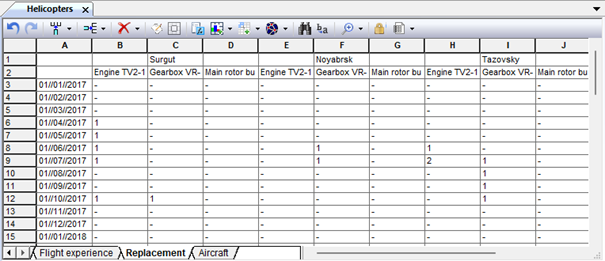
Fig. 9.82. Numerical data – simulation experiment results
