EXAMPLES OF WORKING WITH DATA
Each of the examples is accompanied by a description and a link to the workbook with the implementation.
Using simulation models of tabular type
Modeling of expenses related to car sales in the salon Upload
The following example from the practice of a car dealership is posted on the Internet. In the last hundred months, the sales volume at the dealership ranges from 5 to 11 new cars per month. The salon manager orders 25 cars each time and makes a new order when the stock in the store is reduced to 10 cars. A new order can be made only after the previous one has been completed. We will simulate this strategy for 24 months. Let's perform a Monte Carlo simulation by setting car sales for a month by a random number with the given parameters of the distribution law.We believe that:
a) the initial stock is 30 cars
b) the cost of storing one car is 550,000 rubles per month.
c) one missed sale brings an average loss of 3,330,000 rubles.
d) one order costs 500,000 rubles.
Modeling tasks:
1. How many orders will have to be made in two years?
2. What are the costs associated with this strategy (thousand rubles)?
Let's create a new workbook and insert a simulation sheet there. Let's call it "Imitation of sales". In this sheet, we will create 6 special controller cells necessary for sales modeling (Fig. 9.12).
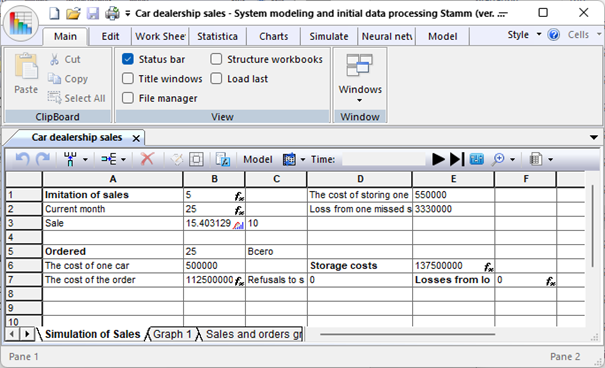
Figure 9.12. Simulation sheet for sales modelling
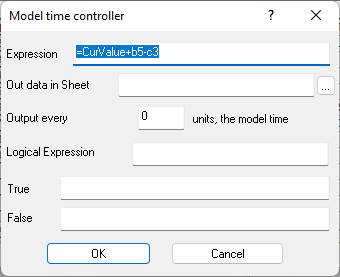
Figure 2. Formula in cell B1
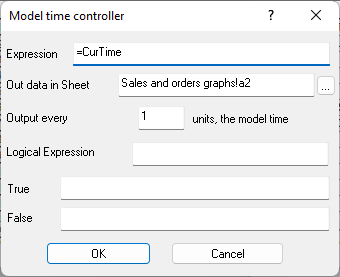
Figure 9.14. Formula in cell B2
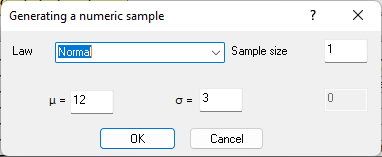
Figure 9.15. Formula in cell B3
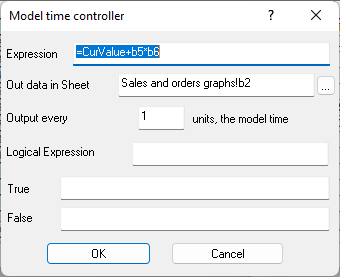
Figure 9.16. Formula in cell B7
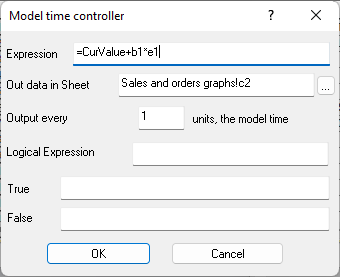
Figure 9.17. Formula in cell E6
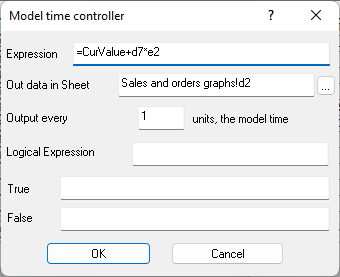
Figure 9.18. Formula in cell F7
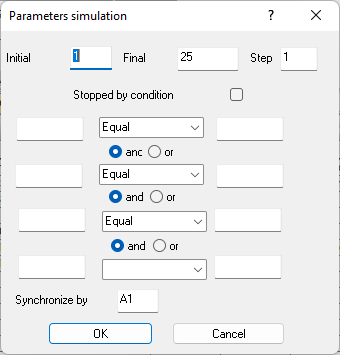
Figure 9.19. Model Parameters
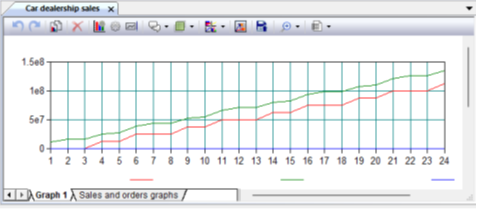
Figure 9.20. Cost change graphs

Figure 9.21. Simulation results
Modeling of repair of mechanisms in the workshop Upload
The repair shop performs preventive inspection and repair of some mechanisms. Of all the mechanisms received by the repair service, 30% are mechanisms of type A, 50% – type B, 20% – type C. The mechanism of type A includes 10 parts that require inspection; the mechanism of type B includes six such parts, type C – four parts. The number of parts requiring replacement in each of the mechanisms can be any. For example, in a type A mechanism, the number of parts requiring replacement can range from 0 to 10 (with the same probability). For each replaced part, the customer pays the repair shop 5 den. units. In addition, the customer pays 10 monetary units for the inspection of mechanism A. units, for the inspection of the mechanism B – 8 monetary units, for the inspection of the mechanism C – 14 monetary units. Create an algorithm and a program (based on the Monte Carlo method) to determine the following values: – the probability that all parts will need to be replaced in the mechanism; – the average revenue of the workshop from the inspection and repair of one mechanism. The problem was solved using a macro written in VBA for Excel, implementing the Monte Carlo method. The implementation of this task in the Stamm system is presented below. The simulation sheet of the corresponding workbook contains 4 controller cells, which are random number generators distributed according to a given law, and 9 controller cells "Calculated expression" (Fig. 9.22).
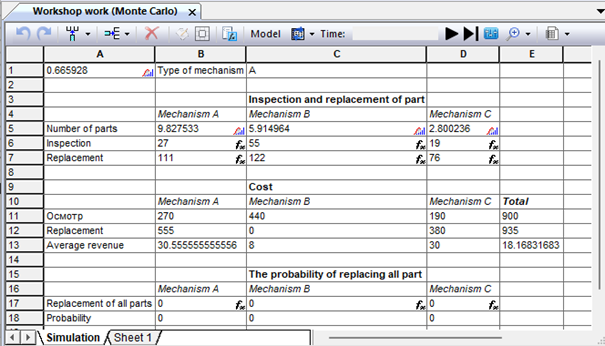
Figure 9.22. The sheet of simulation of inspections and replacement of parts
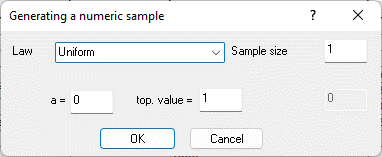
Figure 9.23. Controller cell B1
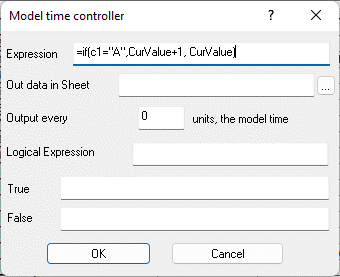
Figure 9.24. Formula in cell B6
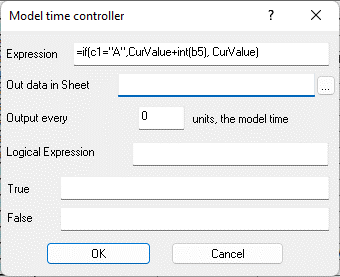
Figure 9.25. Formula expression in cell B7
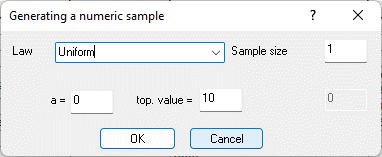
Figure 9.26. Generation of a random variable in cell B5
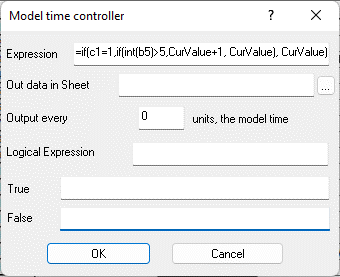
Figure 9.27. Formula in cell B17
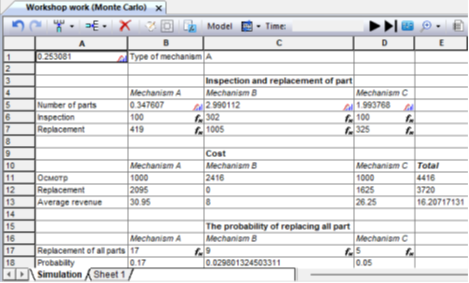
Fig. 9.28. Simulation results
